本当は怖いSVMと交差検証

概要

　SVMと交差検証を組み合わせて使うと、たとえ交差検証で高いスコアが出て汎化性能確保できた！　と思っても想像とかけ離れた分離超平面になっていることがままある。

　なのでこの組み合わせは少し怖いということを説明する。

コード

　irisを分類します。二次元で決定境界を可視化するために、irisを主成分分析を使って2次元に落としておきます。

　GridSearchCVを使って交差検証し、ベストパラメータを探ります。その後、ベストパラメータの分類器で、平面上で散布図と決定境界を可視化してみます。

　ちょっと長いけど、ざっくり読んでみてください。

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt

from sklearn.svm import SVC
from sklearn.model_selection import GridSearchCV
from sklearn.decomposition import PCA
from sklearn.datasets import load_iris

def main():
    # データの準備
    iris = load_iris()
    X, y = PCA(2).fit_transform(iris.data), iris.target

    # GridSearchCVの準備
    svm = SVC()
    params = {"C":10**np.arange(-3, 3, dtype=float),
              "gamma":10**np.arange(-3, 3, dtype=float)}
    gscv = GridSearchCV(svm, params, cv=8, iid=False, 
                        return_train_score=False,
                        verbose=1, n_jobs=-1)
    gscv.fit(X, y)

    # GridSearchCVの結果を表示する
    result_df = pd.DataFrame(gscv.cv_results_)
    print(result_df[["param_C", "param_gamma",
                     "rank_test_score", "mean_test_score"]
                ][result_df["rank_test_score"]==1])

    # 最良推定器をclfに代入
    clf = gscv.best_estimator_
    
    # 可視化の準備
    xmin, xmax, ymin, ymax = (X[:,0].min()-1, X[:,0].max()+1,
                              X[:,1].min()-1, X[:,1].max()+1)    
    x_ = np.arange(xmin, xmax, 0.01)
    y_ = np.arange(ymin, ymax, 0.01)
    xx, yy = np.meshgrid(x_, y_)

    # 予測
    zz = clf.predict(np.stack([xx.ravel(), yy.ravel()], axis=1)
                 ).reshape(xx.shape)

    # 可視化
    plt.pcolormesh(xx, yy, zz, cmap="winter", alpha=0.1, shading="gouraud")
    plt.scatter(X[:, 0], X[:, 1], c=y, edgecolors='k', cmap="winter")
    plt.savefig("result.png")

if __name__ == "__main__":
    main()

結果

　printされた結果は良さげなものでした。

   param_C param_gamma  rank_test_score  mean_test_score
22       1          10                1         0.972222

　0.972222なら悪くないaccuracyです。

　しかし、出力された画像は思っていたものとは違いました。

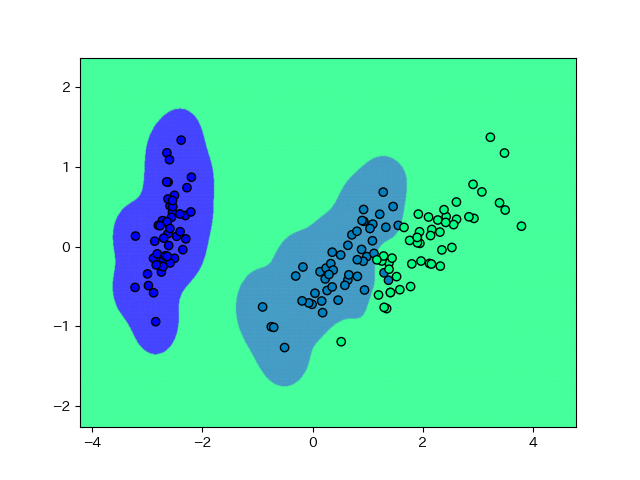
　こわっ。どう考えてもこういうデータではないと思いますが、こういうことが現実に起こります。(-1.5, 0)あたりにデータが来たら、青かねずみ色のどちらかの色のグループに分類されてほしいところですが、実際は緑になってしまう訳です。

　ちょっと信頼ならないですね、SVM。

怖くない線形SVM

　ついでにいろいろな分類器を見てみます。

　LinearSVCをimportし、「# GridSearchCVの準備」以下「# 最良推定器をclfに代入」の上までを次のように書き換える。

    # GridSearchCVの準備
    svm = LinearSVC()
    params = {"C":10**np.arange(-3, 3, dtype=float)}
    gscv = GridSearchCV(svm, params, cv=8, iid=False, 
                        return_train_score=False,
                        verbose=1, n_jobs=-1)
    gscv.fit(X, y)

    # GridSearchCVの結果を表示する
    result_df = pd.DataFrame(gscv.cv_results_)
    print(result_df[["param_C",
                     "rank_test_score", "mean_test_score"]
                ][result_df["rank_test_score"]==1])

　結果。

  param_C  rank_test_score  mean_test_score
4      10                1         0.960317

　accuracyはわずかに下がるだけ。

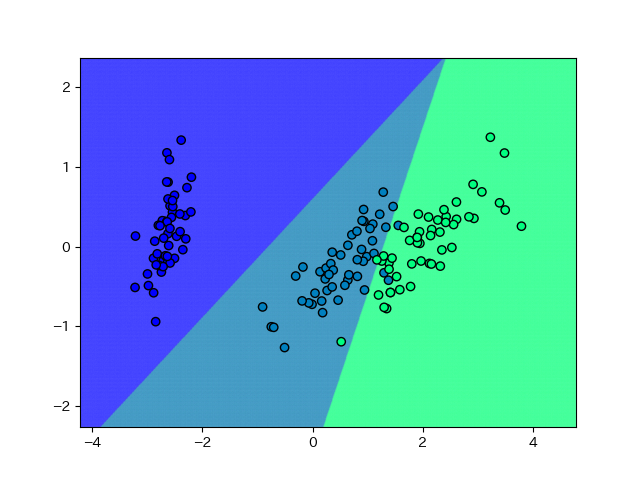
　はるかに納得感の高い結果になっています。こういうことがあるので、ほぼ線形分離可能なことがわかっているデータは、まずは線形なモデルで試すことがおすすめです。非線形なモデルで1%とかaccuracyをあげられるとしても、それで未知のデータに対して良い推定ができるかどうかは交差検証ではわからないのです*1。

怖いかどうか悩むランダムフォレスト

　LinearSVCと同様にRandomForestClassifierをimportし、同じ箇所を書き換えます。

    # GridSearchCVの準備
    clf = RandomForestClassifier(n_jobs=-1)
    params = {"n_estimators":10**np.arange(3),
              "min_samples_leaf":[1,2]}
    gscv = GridSearchCV(clf, params, cv=8, iid=False, 
                        return_train_score=False,
                        verbose=1, n_jobs=-1)
    gscv.fit(X, y)

    # GridSearchCVの結果を表示する
    result_df = pd.DataFrame(gscv.cv_results_)
    print(result_df[["param_n_estimators", "param_min_samples_leaf",
                     "rank_test_score", "mean_test_score"]
                ][result_df["rank_test_score"]==1])

　性能。SVMと比べると少し低下するかな。理由はよくわからないけど、木の本数10本で葉の最小サンプル数2のときが最高性能（本当になんで？　基本的に木が多い方が性能が高いはずなのだが・・・）。

  param_n_estimators param_min_samples_leaf  rank_test_score  mean_test_score
4                 10                      2                1         0.953373

　可視化。

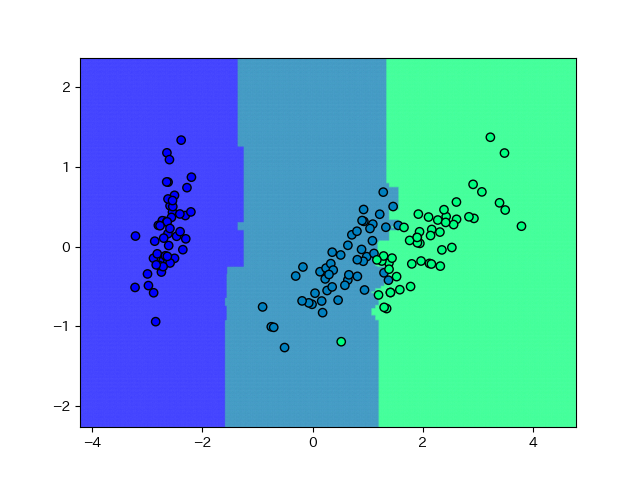
　この状態ではrefitしているので、accuracyは1になるはずです。さて、ランダムフォレストの特徴は、決定木なので軸と90度の直線の組み合わせで決定境界が表現されることです。また、少ない分割でエントロピーが下がるような決定境界を追求していくので、データの全体の傾向はあまり見てくれません。

　それでもSVMよりはマシな感じでしょうか。

怖くない気がする多層パーセプトロン

　疲れてきたので最後。やり方は上と同じ。

    # GridSearchCVの準備
    clf = MLPClassifier(max_iter=3000)
    params = {"hidden_layer_sizes":[(5*x,) for x in range(1, 5)]}
    gscv = GridSearchCV(clf, params, cv=8, iid=False, 
                        return_train_score=False,
                        verbose=1, n_jobs=-1)
    gscv.fit(X, y)

    # GridSearchCVの結果を表示する
    result_df = pd.DataFrame(gscv.cv_results_)
    print(result_df[["param_hidden_layer_sizes",
                     "rank_test_score", "mean_test_score"]
                ][result_df["rank_test_score"]==1])

　同率一位が3つもありました。ま、どれでも良いか。

  param_hidden_layer_sizes  rank_test_score  mean_test_score
1                    (10,)                1          0.96627
2                    (15,)                1          0.96627
3                    (20,)                1          0.96627

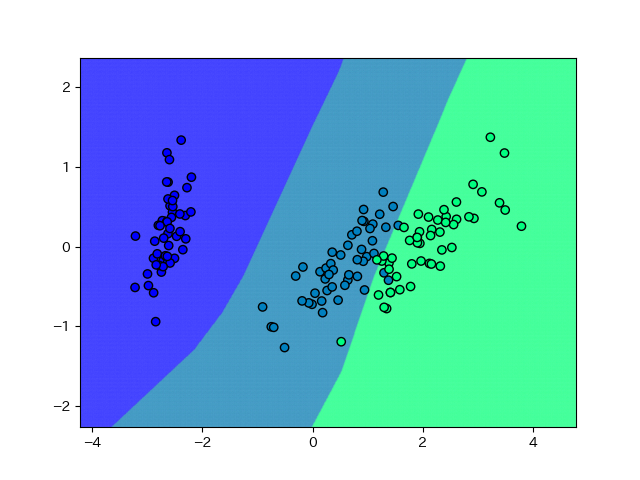
　まともな感じ。右側の決定境界はちょっと甘いかなー、という気はします。

　ただしパラメータ数の少ない隠れ層1層の多層パーセプトロンだからこれくらいの素直な結果に落ち着くのであって、深層学習は油断するとすぐ過学習するので注意が必要です。

SVMも怖くない！

　汎化重視のパラメータにすれば変なことにはならないので安心してください。基本的にCもgammaも低ければ低いほど過学習しづらくなります。

　今までと同じ箇所をこう書き換える。

    # SVMをfit
    clf = SVC(C=1, gamma=0.2)
    clf.fit(X, y)

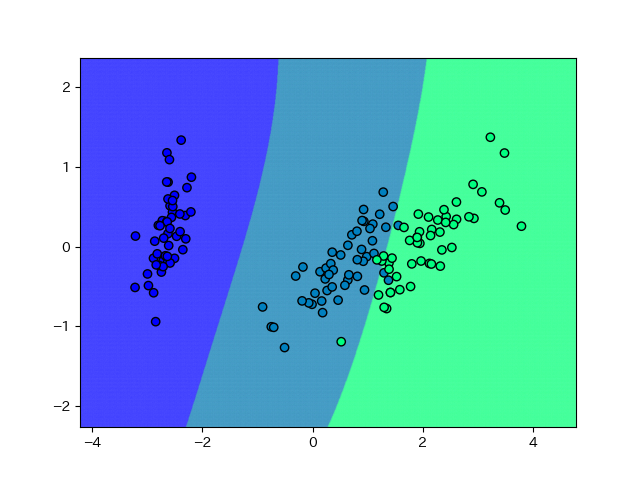
　別に問題ないですよね。SVMそのものはこのようにパラメータで自由に分離超平面の複雑さを調整できる、優れた分類器です。

　ただし、交差検証で機械的にパラメータを決めてしまうとあまり良くない結果を招く可能性がある訳です。

現実的な話

　二次元で見ているから違和感があるのであって、高次元空間はサクサクメロンパン問題があるのでまた異なった挙動になります。

　↓サクサクメロンパン問題

次元の呪い、あるいは「サクサクメロンパン問題」 - 蛍光ペンの交差点[別館]

　直感的な理解は難しいと思いますが、こういうことが問題になるケースは少ないということはなんとなくわかります。

　とはいえ、「交差検証して最高性能だったSVMを投入したらトンチンカンな結果を出してくる」みたいなことが実際に起こらないとも限らないので、ある程度は注意した方が良いでしょう。

まとめ

　SVMはパラメータ設定を過学習するようにしたとき、他の手法と比べても群を抜いて変な結果になるのですが、何が駄目なんでしょうね。やっぱりカーネル使ってるからか。

　ちょっと注意が要るよなー、というお話でした。

*1:手持ちのデータの分布に依存する話ですが。未知のデータなんてないぜ！　といえるくらい豊富なデータがあればそれはそれで構いません

静かなる名辞

pythonとプログラミングのこと