【python】numpyで主成分分析を実装してみた

　numpyでPCA（principal component analysis：主成分分析）を実装してみました。自分の理解を深めるためです。

　sklearnに実装されているものと同じ結果を出すことを目標にしました。最終的には上手く行きました。

概要
実装
結果
まとめ

概要

　主成分分析のアルゴリズムの解説は他に譲ります。これは実装してみた記事です。

　実装のやり方は色々あるようですが、一番基本的な（だと思う）共分散行列の固有値と固有ベクトルを求める方法で行きます。

　やるべきこととしては、

データをセンタリングする（列ごとに平均を引く）
共分散行列を計算する
固有値と固有ベクトルを計算
データを固有ベクトルを使って写像する

　これらを実装すれば行けるはずです。というか、これで行くことにしました。

実装

　書いたソースコードを以下に示します。

# coding: UTF-8

import numpy as np

from sklearn.datasets import load_iris
from sklearn.decomposition import PCA

import matplotlib.pyplot as plt

class MyPCA:
    def __init__(self, n_components=2):
        self.n_components = n_components

    def fit_transform(self, X):
        """横着してfit_transformしか実装してない
        """

        # 平均を0にする
        X = X - X.mean(axis=0)

        # 共分散行列を作る
        self.cov_ = np.cov(X, rowvar=False)
        
        # 固有値と固有ベクトルを求めて固有値の大きい順にソート
        l, v = np.linalg.eig(self.cov_)
        l_index = np.argsort(l)[::-1]
        self.l_ = l[l_index]
        self.v_ = v[:,l_index] # 列ベクトルなのに注意

        # components_（固有ベクトル行列を途中まで取り出す）を作る
        self.components_ = self.v_[:,:self.n_components].T

        # データとcomponents_をかける
        # 上と下で二回転置してるのアホ・・・
        T = (np.mat(X)*(np.mat(self.components_.T))).A

        # 出力
        return T

def main():
    iris = load_iris()

    pca = PCA(n_components=2)
    sklearn_X = pca.fit_transform(iris.data)

    my_pca = MyPCA()
    my_X = my_pca.fit_transform(iris.data)

    print(pca.explained_variance_)
    print(my_pca.l_)

    print(pca.components_)
    print(my_pca.components_)

    plt.figure()
    plt.scatter(sklearn_X[:,0], sklearn_X[:,1], c=iris.target/3)
    plt.savefig("sklearn_resut.png")

    plt.figure()
    plt.scatter(my_X[:,0], my_X[:,1]*-1, c=iris.target/3)
    plt.savefig("my_result.png")

if __name__ == "__main__":
    main()

　numpyを使ったので簡単に書けました。アルゴリズム部分はコメントで解説を入れたので、それを読めばどんな感じかは理解して頂けると思います。

結果

　mainのテキスト出力を見ると、次のようになっていました。

# 固有値
[4.22484077 0.24224357]
[4.22484077 0.24224357 0.07852391 0.02368303]

# components_
[[ 0.36158968 -0.08226889  0.85657211  0.35884393]
 [ 0.65653988  0.72971237 -0.1757674  -0.07470647]]
[[ 0.36158968 -0.08226889  0.85657211  0.35884393]
 [-0.65653988 -0.72971237  0.1757674   0.07470647]]

　固有値が余計に出ちゃってますが、これは別に構いません。また、componentsの2次元目が符号反転していますが、これも特に問題ないこと（のはず）なので無視します。

　自作の方は第二主成分を反転させてプロットしてみました。

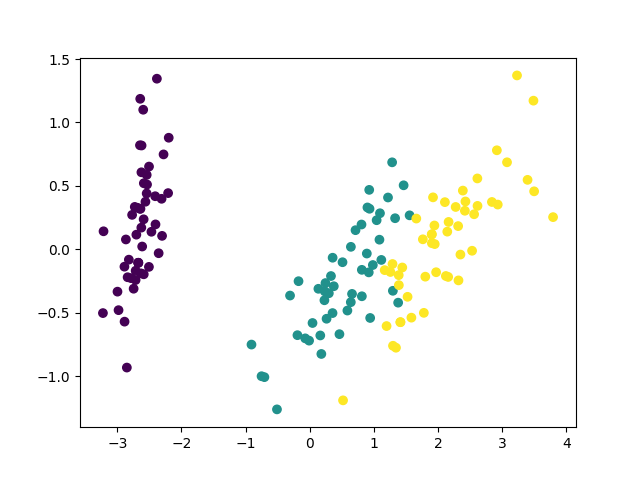
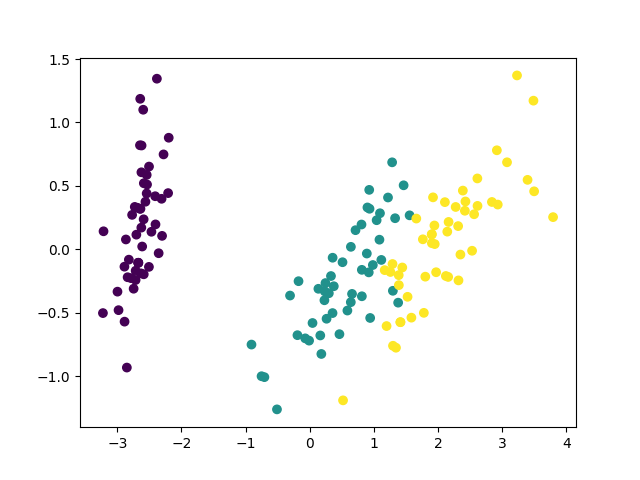
　同じ図を2つ載せるなって怒られそうですが・・・とにかく上手く行ったようです。

まとめ

　numpyで実装してみたら思ったより簡単だったので、これで当分は「わかった気」になれそうです。

　ただ、今回は特異値分解やらなかったので、それはまた宿題ということで・・・。

静かなる名辞

pythonとプログラミングのこと

【python】numpyで主成分分析を実装してみた

概要

実装

結果

まとめ