【python】sklearnのPCAで相関行列を使う

　主成分分析には共分散行列を用いる方法、相関行列を使う方法がある。

　sklearnのPCAを見ると、これに対応するオプションは存在しない。

sklearn.decomposition.PCA — scikit-learn 0.20.1 documentation

　ずっと不思議に思っていたが、ググってたらこんなものを見つけた。

Enhance: PCA options for using Correlation or covariance matrix · Issue #2689 · scikit-learn/scikit-learn · GitHub

　要約：特徴量をスケーリングしてPCAすれば相関行列でやったのと同じことになるよ。PipelineでStandardScalerと組み合わせてね。おわり。

本当か確認する

　確認してみる。

>>> import numpy as np
>>> from sklearn.datasets import load_iris
>>> from sklearn.preprocessing import StandardScaler
>>> from sklearn.decomposition import PCA
>>> from sklearn.pipeline import Pipeline
>>> iris = load_iris()
>>> pca = PCA(n_components=2)
>>> pca.fit(iris.data)
PCA(copy=True, iterated_power='auto', n_components=2, random_state=None,
  svd_solver='auto', tol=0.0, whiten=False)
>>> pca.get_covariance()
array([[ 0.67919741, -0.03258618,  1.27066452,  0.5321852 ],
       [-0.03258618,  0.18113034, -0.31863564, -0.13363564],
       [ 1.27066452, -0.31863564,  3.11934547,  1.28541527],
       [ 0.5321852 , -0.13363564,  1.28541527,  0.58961806]])
>>> ss = StandardScaler()
>>> p = Pipeline([("scaler", ss), ("pca", pca)])
>>> p.fit(iris.data)
Pipeline(memory=None,
     steps=[('scaler', StandardScaler(copy=True, with_mean=True, with_std=True)), ('pca', PCA(copy=True, iterated_power='auto', n_components=2, random_state=None,
  svd_solver='auto', tol=0.0, whiten=False))])
>>> p.steps[1][1].get_covariance()
array([[ 0.9779242 , -0.10104477,  0.87069468,  0.86134879],
       [-0.10104477,  1.00395722, -0.41916911, -0.37286994],
       [ 0.87069468, -0.41916911,  1.04639367,  0.93676197],
       [ 0.86134879, -0.37286994,  0.93676197,  0.99857055]])
>>> np.corrcoef(iris.data, rowvar=False)
array([[ 1.        , -0.10936925,  0.87175416,  0.81795363],
       [-0.10936925,  1.        , -0.4205161 , -0.35654409],
       [ 0.87175416, -0.4205161 ,  1.        ,  0.9627571 ],
       [ 0.81795363, -0.35654409,  0.9627571 ,  1.        ]])

　違うじゃん。妥当そうなのはnumpyの結果だが（対角成分が1になってる）、とりあえずしょうがないのでスケーリングしたデータの共分散をnumpyで計算してみる。

>>> np.cov(ss.fit_transform(iris.data), rowvar=0, bias=1)
array([[ 1.00671141, -0.11010327,  0.87760486,  0.82344326],
       [-0.11010327,  1.00671141, -0.42333835, -0.358937  ],
       [ 0.87760486, -0.42333835,  1.00671141,  0.96921855],
       [ 0.82344326, -0.358937  ,  0.96921855,  1.00671141]])
>>> np.cov(ss.fit_transform(iris.data), rowvar=0, bias=1)
array([[ 1.        , -0.10936925,  0.87175416,  0.81795363],
       [-0.10936925,  1.        , -0.4205161 , -0.35654409],
       [ 0.87175416, -0.4205161 ,  1.        ,  0.9627571 ],
       [ 0.81795363, -0.35654409,  0.9627571 ,  1.        ]])

　標本分散はnp.corrcoefと等価だ。

　ここまでやったところでもう一回ドキュメントを読み、PCA.get_covariance()の結果が「Estimated covariance of data.」であり、厳密ではないことに気づいたので、問題は解決した。

　理論的にこうなる理由は、説明しようと思えばできるのだと思いますが、今回は大変なので触れません。

irisでやってみる

　irisの可視化にそれぞれを使ってみる。コードを以下に示す。

# coding: UTF-8

from sklearn.datasets import load_iris
from sklearn.preprocessing import StandardScaler
from sklearn.decomposition import PCA
from sklearn.pipeline import Pipeline

import matplotlib.pyplot as plt

def main():
    iris = load_iris()

    ss = StandardScaler()
    pca = PCA(n_components=2)
    p = Pipeline([("scaler", ss), ("pca", pca)])
    
    X = pca.fit_transform(iris.data)

    plt.figure()
    plt.scatter(X[:,0], X[:,1], c=iris.target/3)
    plt.savefig("iris_cov_pca.png")

    X = p.fit_transform(iris.data)

    plt.figure()
    plt.scatter(X[:,0], X[:,1], c=iris.target/3)
    plt.savefig("iris_corr_pca.png")

if __name__ == "__main__":
    main()

　結果は、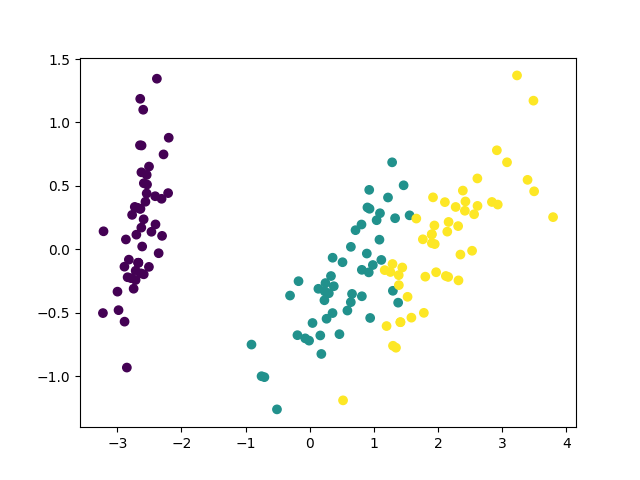

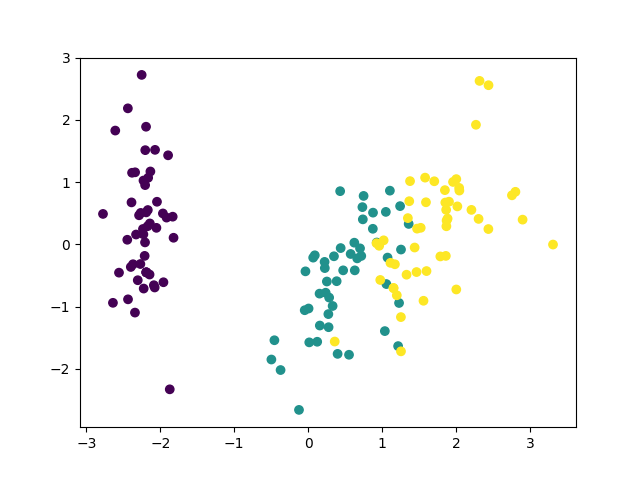
　こうして見ると相関行列はあまりメリットがないように見えますが、実際には相関行列の方が良いタスクは色々あるようです。相関行列を使うことでbiplotが上手く行っているという例を出しているページを載せておきます。
PCA on correlation or covariance? - Cross Validated

まとめ

　とりあえずできることはわかったので良しとする。

　でも、「pipelineで出来るから要らねーよ」ってつもりらしいけど、ぶっちゃけオプション一つでできた方が親切だと思った（小並感）。

静かなる名辞

pythonとプログラミングのこと

【python】sklearnのPCAで相関行列を使う

本当か確認する

irisでやってみる

まとめ